플로이드-워셜(Floid-Warshall) 알고리즘

플로이드-워셜(Floid-Warshall) 알고리즘

플로이드-워셜(Floid-Washal) 알고리즘은 모든 노드간의 최단 거리를 구하는 알고리즘이다. 해당 알고리즘은 두 노드 간의 최단 경로를 최적이 될 때까지 점진적으로 개선시킴으로써 최단경로를 찾는다.
해당 알고리즘의 시간복잡도는 O(n^3)이다.

알고리즘 과정

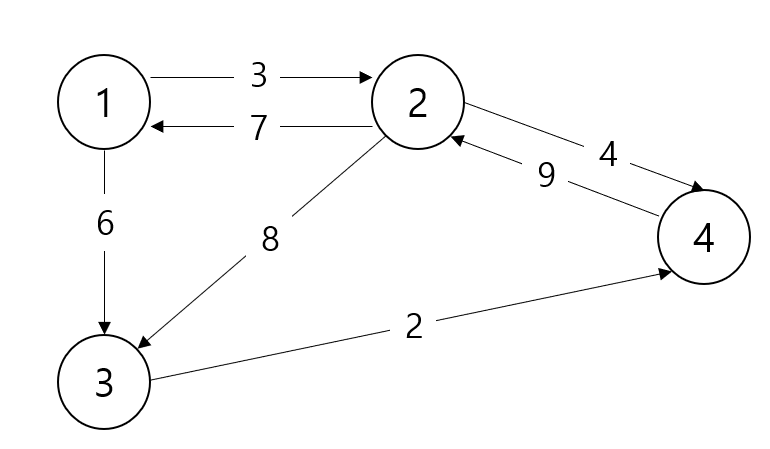
위의 그래프에서 노드에서 다른 노드로 가는 비용을 이차원 배열로 구성하여 표시하면 다음과 같다. 해당 표에서 INF는 특정 노트에서 다른 노드로 가는 길이 없을 경우를 의미하며, 자기자신에게 이동하는 경우에 대한 비용은 0으로 할당한다.

	N1	N2	N3	N4
N1	0	3	6	INF
N2	7	0	8	4
N3	INF	INF	0	2
N4	INF	9	INF	0

노드 1을 경유하는 경우

노드 1을 경우하여 다른 노드로 가는 이동하는 최단거리를 구하는 과정에서 개선되는 내용은 없다.

	N1	N2	N3	N4
N1	0	3	6	INF
N2	7	0	8	4
N3	INF	INF	0	2
N4	INF	9	INF	0

노드 2를 경유하는 경우

노드 2를 경우하여 다른 노드로 가는 과정에서 1 -> 4번 노드, 4 -> 1번 노드, 4 -> 3번 노드로 가는 최단거리 비용이 개선된다.
4 -> 1번 노드로 가는 비용이 기존 INF이 9 + 7 = 16 보다 크기 때문에 최단거리 비용이 16으로 개선되며, 4 -> 3번 노드로 가는 비용도 동일하게 개선된다.

	N1	N2	N3	N4
N1	0	3	6	7
N2	7	0	8	4
N3	INF	INF	0	2
N4	16	9	17	0

최종 결과

이러한 과정을 노드의 갯수만큼 수행하며, 위의 그래프에서는 노드 3, 노드 4를 경유하는 경우에 대하여 최단거리 비용에 대하여 개선된다.

이러한 과정을 과정을 통하여 최종적으로 다음과 같은 결과가 생성된다.

	N1	N2	N3	N4
N1	0	3	6	7
N2	7	0	8	4
N3	18	11	0	2
N4	16	9	17	0

구현

플로이드-워셜 알고리즘의 내용을 Javascript 코드로 작성시 다음과 같다.

function floydWarshall(dist) {
  const len = dist.length;
  for (let k = 0; k < len; k += 1) {
    for (let i = 0; i < len; i += 1) {
      for (let j = 0; j < len; j += 1) {
        dist[i][j] = Math.min(dist[i][j], dist[i][k] + dist[k][j])
      }
    }
  }
}

const INF = Infinity;
const graph = [
  [0, 3, 6, INF],
  [7, 0, 8, 4],
  [INF, INF, 0, 2],
  [INF, 9, INF, 0]
];

floydWarshall(graph);
console.debug(graph);


// [ [ 0, 3, 6, 7 ], [ 7, 0, 8, 4 ], [ 18, 11, 0, 2 ], [ 16, 9, 17, 0 ] ]